3,210 reads
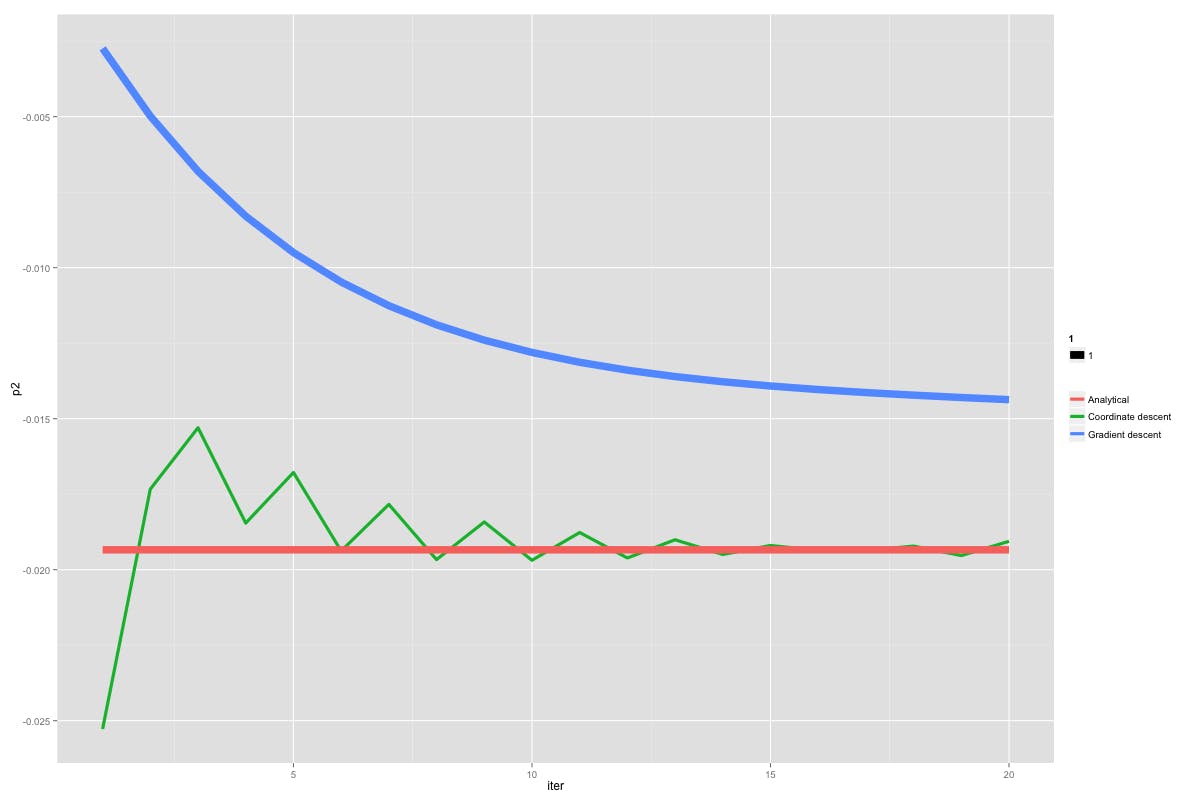
Gradient descent vs coordinate descent
by
April 12th, 2017
Audio Presented by

I do stuff with computers, host data science at home podcast, code in Rust and Python
About Author
I do stuff with computers, host data science at home podcast, code in Rust and Python