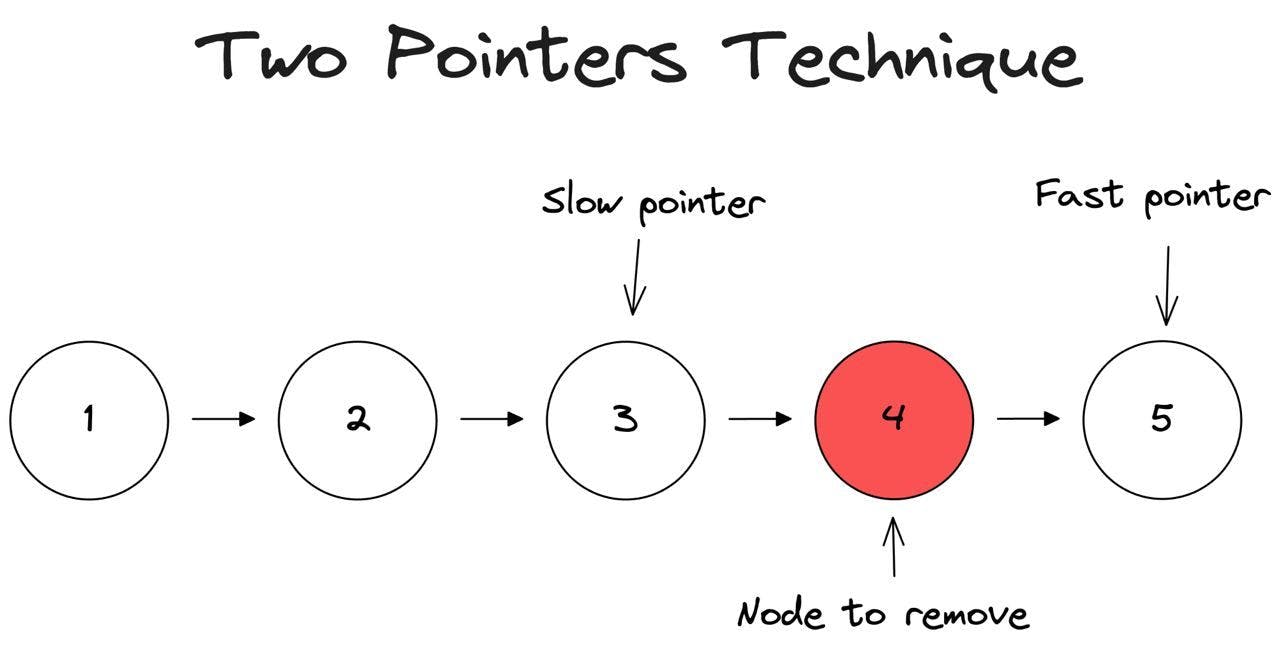
22,374 reads
Optimizing List Manipulation: Two Pointers Technique
by
February 9th, 2023
Audio Presented by

Senior Software Engineer. I work with high-performance distributed systems and big data processing.
Story's Credibility

About Author
Senior Software Engineer. I work with high-performance distributed systems and big data processing.