220 reads
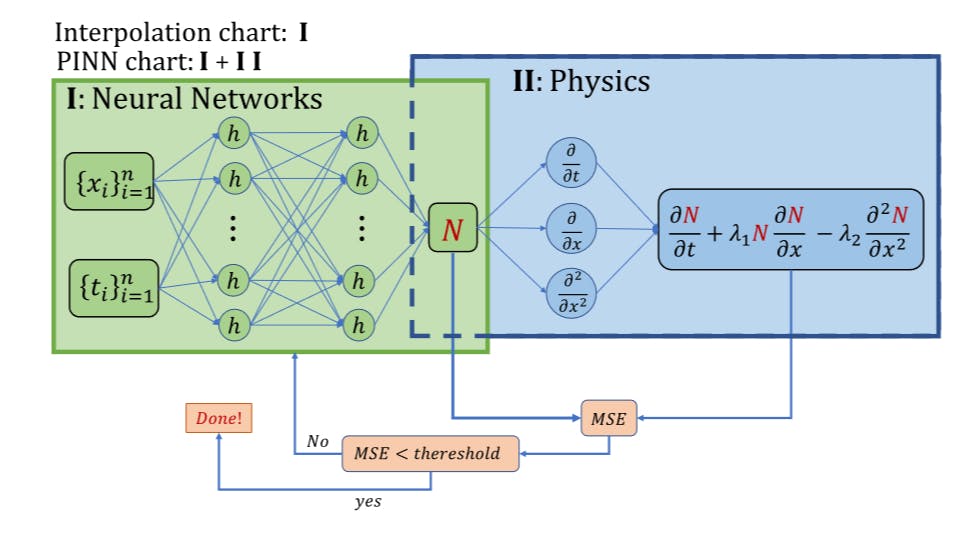
Physics-Informed with Power-Enhanced Residual Network: PINN for Solving Inverse Burgers’ Equation
by
February 28th, 2024
Audio Presented by

#1 Publication focused exclusively on Interpolation, ie determining value from the existing values in a given data set.
About Author
#1 Publication focused exclusively on Interpolation, ie determining value from the existing values in a given data set.