200 reads
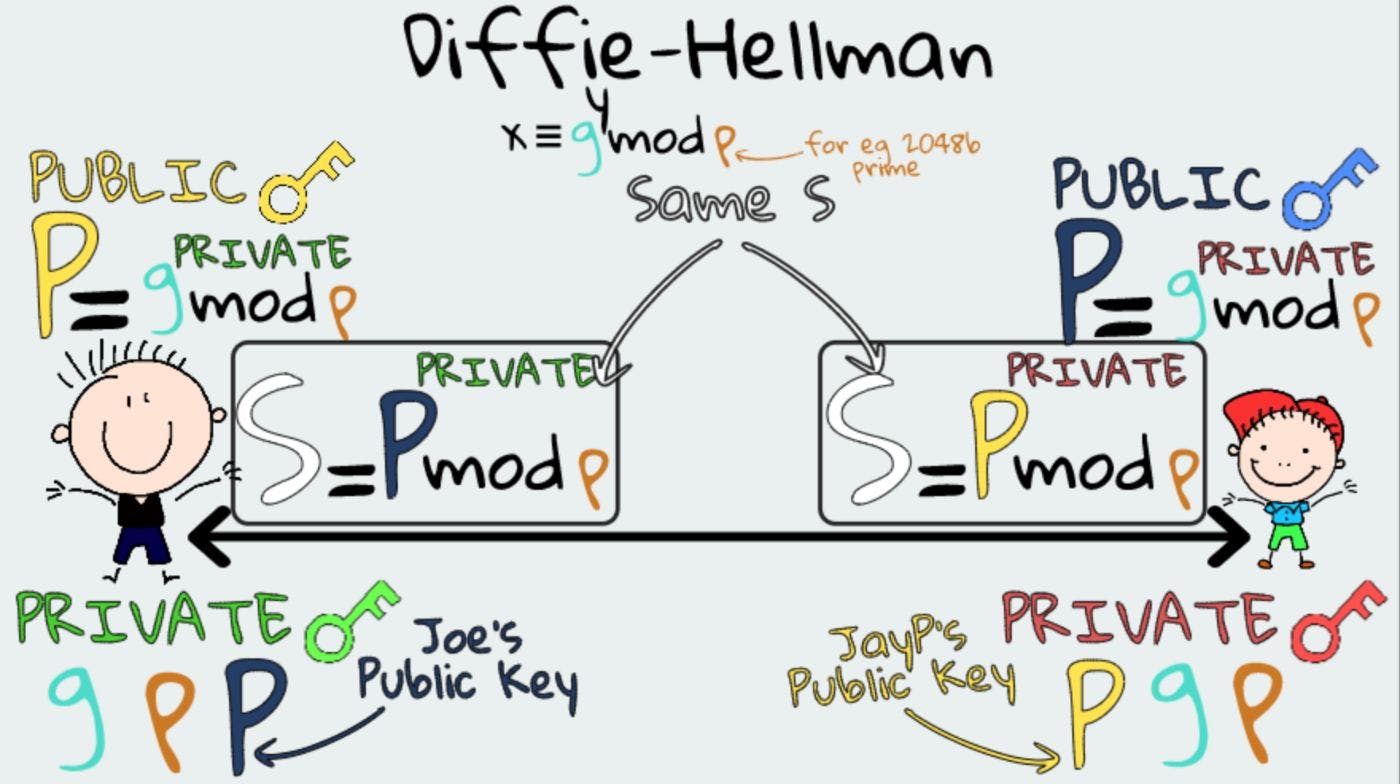
Diffie-Hellman & Its Simple Maths: A Quick Explanation for Web Developers🙆🏻♂️
by
August 22nd, 2023
Audio Presented by

Continuously read and learn about web and mobile development 🧑🏻💻. Also loves meat 🍗.
About Author
Continuously read and learn about web and mobile development 🧑🏻💻. Also loves meat 🍗.