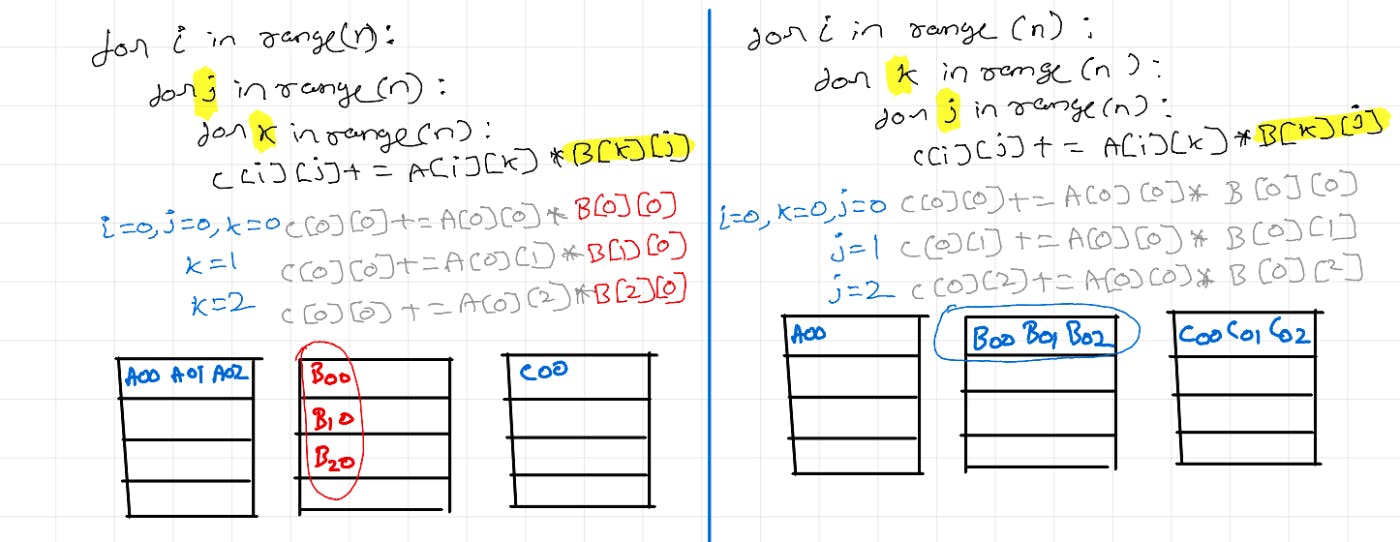
182 reads
How Understanding CPU Caches Can Supercharge Your Code: 461% Faster MatMul Case Study
by
April 25th, 2024
Audio Presented by

🧑💻 Software Engineer |📍Berlin 🇩🇪 | 📚 https://venkat.eu | 💬 https://twitter.com/Venkat2811
Story's Credibility

About Author
🧑💻 Software Engineer |📍Berlin 🇩🇪 | 📚 https://venkat.eu | 💬 https://twitter.com/Venkat2811